1800-150-456-789
FlagBACK
Flag Magical Mathematics[Interesting Approach]>
question mark

pranay -askiitians expert , 14 Years ago
Grade 12
anser 4 Answers
Askiitians_Expert Yagyadutt

Last Activity: 14 Years ago

Hii pranav !

 

 

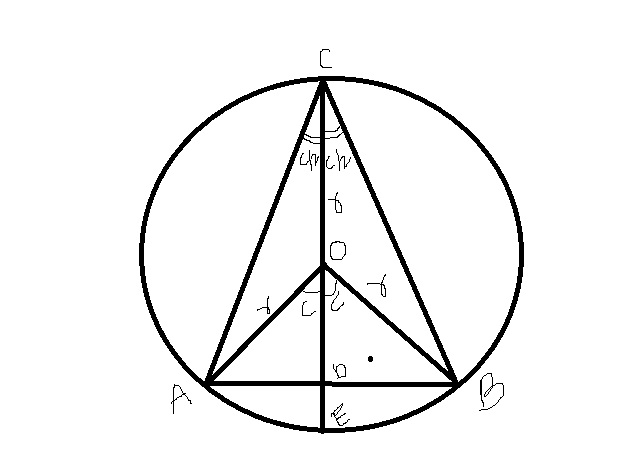1206_23490_Untitled.jpg

 

Ok now look at the picture....I guess you remeber a theorem ...we have studied in the class IX ...If AB and CE are the two chord intersecting inside the circle...at point D ..then

AD.DB = CD.DE --------------------(1) ...

 

Now Since the length of chord is always positve...so AM > GM is applied ...

 

(AD + DB ) /2  > =  root( AD.DB)

(AD + DB ) > = 2 root( CD.DE) ---------------2(1)

 

So maximum value of CD.DE =  (AD + DB)^2 / 4    [ is it clear ? ]

 

Now our aim is to find out what will be the value of  AD + DB ...

 

Look in the figure i have drawn ...  

 

AD = r sinc

DB = r sinc   

 

The angle AOD = c ...( because of the theorem that ...angle at the centre is twice the angle at any portion on the circle )

 

So ...AD + DB = 2 rsinc

(AD + DB )^2 = 4.r^2sin^2(c)

(AD + DB ) ^2 / 4  =  r^2.sin^2(c)

 

Hence  maximum value of  CD.DE as declared above ....=  r^2.sin^2(c) .....since sin^2(c) is variable ...if c is variable...then maximum value of CD.DE =  r^2   ( because sin^2(c) = 1 )  where r is the radius of the circle..which you have not specified in the question....

 

Now let me know...if the answer is wrong !

 

Regards

Yagya

 

askiitians_expert

pranay -askiitians expert

Last Activity: 14 Years ago

but the answer is given as c2/4 i.e. (AB)2/4

Askiitians_Expert Yagyadutt

Last Activity: 14 Years ago

No Problem dude !

 

Your given answer is also correct...and what i have written is also correct  ...

 

Look   CD.DE  = AD.DB  

 

Maximum value of CD.DE will be equal to maximum value of AD.DB ...isn't ?

 

(AD + DB)/2  >= root (AD.DB)  ( according to AM >GM )

 

so  Maximum case....AD.DB = (AD+DB)^2/4   => AD.DB = (AB)^2/4   [ you got it ]

pranay -askiitians expert

Last Activity: 14 Years ago

thanks much plz accept my friend request

Provide a better Answer & Earn Cool Goodies

Enter text here...
star
LIVE ONLINE CLASSES

Prepraring for the competition made easy just by live online class.

tv

Full Live Access

material

Study Material

removal

Live Doubts Solving

assignment

Daily Class Assignments


Ask a Doubt

Get your questions answered by the expert for free

Enter text here...

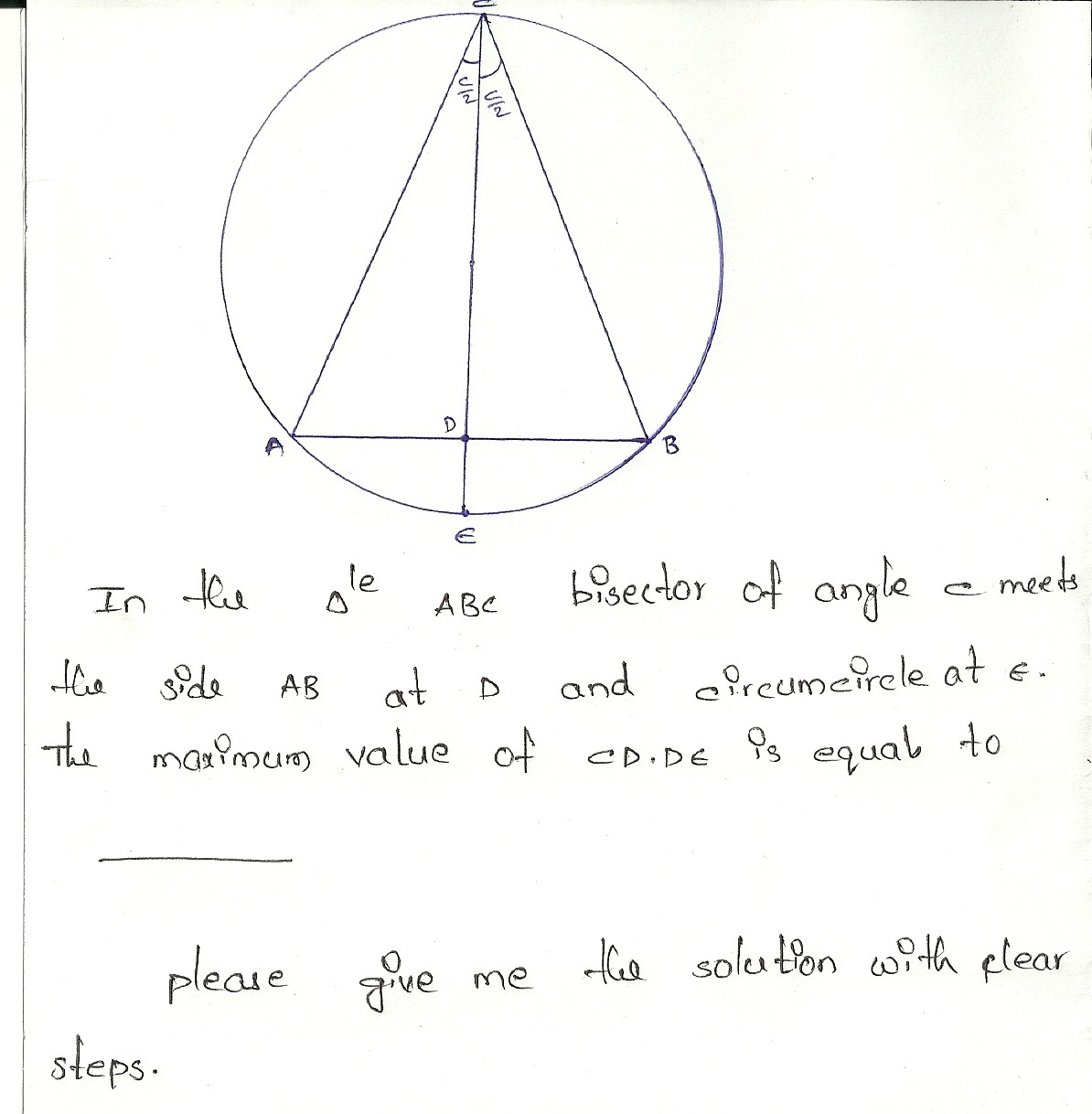
Other Related Questions on Magical Mathematics[Interesting Approach]

question mark
Given that (1+5x)⁴ = 1 + Px + Qx² + Rx³ +..... Find the values of P - 2Q + 3R
Magical Mathematics[Interesting Approach]
1 Answer Available

Last Activity: 2 Years ago

question mark
9 men and 15 boys working 10 hours a day can make 12 pillars in 42 days, in how many days will 12 men and 22 boys working 8 hours a day can make pillars 4 times the previous number?
Magical Mathematics[Interesting Approach]
1 Answer Available

Last Activity: 2 Years ago

question mark
In the given figure, PQ is a tangent at a point C to a circle with centre O. If AB is a diameter, find angle PCA + angle BCQ?
Magical Mathematics[Interesting Approach]
0 Answer Available

Last Activity: 2 Years ago

question mark
for any two sets A and B (A-B)U(B-A)U (A intersection B)
Magical Mathematics[Interesting Approach]
0 Answer Available

Last Activity: 2 Years ago

question mark
If someone has got 150 out of 200 marks in term 1 exam and 160 out of 200 marks in term 2 exam then what is the percentage in30:70
Magical Mathematics[Interesting Approach]
0 Answer Available

Last Activity: 3 Years ago